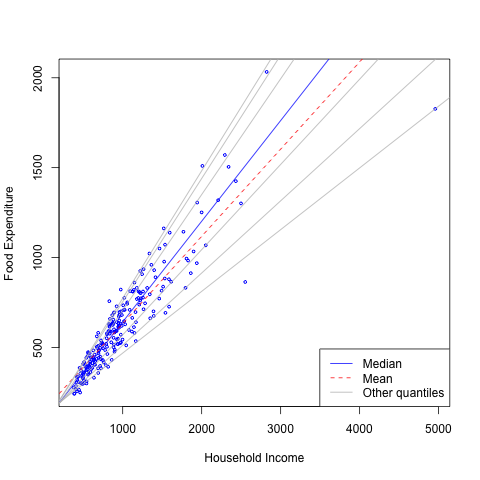
- Engel data on food expenditure vs household income for a sample of 235 19th century working class Belgian households.
- More information from quantile regression
- Slope change
- Skewness
- Less sensitive to heterogeneity and outliers
Minzhao Liu, Department of Statistics, The University of Florida
Mike Daniels, Department of Integrative Biology, The University of Texas at Austin

A missing data pattern is monotone if, for each individual, there exists a measurement occasion \(j\) such that \(R_1 = ··· = R_{j−1} = 1\) and \(R_j = R_{j+1} = · · · = R_J = 0\); that is, all responses are observed through time \(j − 1\), and no responses are observed thereafter. \(S\) is called follow-up time.
| Subject | T1 | T2 | T3 | T4 | S |
|---|---|---|---|---|---|
| Subject 1 | \(Y_{11}\) | \(Y_{12}\) | 2 | ||
| Subject 2 | \(Y_{21}\) | \(Y_{22}\) | \(Y_{23}\) | \(Y_{24}\) | 4 |
\(\Delta_{ij}\) are subject/time specific intercepts determined by the parameters in the model and are determined by the marginal quantile regressions, \[ \tau = Pr (Y_{ij} \leq \mathbf x_{i}^T \mathbf \gamma_j ) = \sum_{k=1}^J \phi_kPr_k (Y_{ij} \leq \mathbf x_{i}^T \mathbf \gamma_j ) \mbox{ for } j = 1, \] and \[ \begin{align} \tau &= Pr (Y_{ij} \leq \mathbf x_{i}^{T} \mathbf \gamma_j ) = \sum_{k=1}^J \phi_kPr_k (Y_{ij} \leq \mathbf x_{i}^{T} \mathbf \gamma_j ) \\ & = \sum_{k=1}^J \phi_k \int\cdots \int Pr_k (Y_{ij} \leq \mathbf x_{i}^{T} \mathbf \gamma_j | \mathbf y_{ij^{-}} ) p_k (y_{i(j-1)}| \mathbf y_{i(j-1)^{-}}) \nonumber \\ & \quad \cdots p_k (y_{i2}| y_{i1}) p_k(y_{i1}) dy_{i(j-1)}\cdots dy_{i1}. \mbox{ for } j = 2, \ldots, J .\nonumber \end{align} \]
\[ Y_{ij}|\mathbf Y_{ij^{-}}, S_i = k \sim \begin{cases} \textrm{N} \big (\Delta_{ij} + \mathbf y_{ij^{-}}^T \mathbf \beta_{Y,j-1}, \sigma_j \big), & k \geq j ; \\ \textrm{N} \big (\Delta_{ij} + \mathbf y_{ij^{-}}^T \mathbf \beta_{y,j-1} + h_{0}^{(k)}, \sigma_j \big), & k < j ; \\ \end{cases}, \mbox{ for } 2 \leq j \leq J, \]
The observed data likelihood for an individual \(i\) with follow-up time \(S_i = k\) is \[ \begin{align} L_i(\mathbf \xi| \mathbf y_i, S_{i} = k) & = \phi_kp_k (y_k | y_1, \ldots, y_{k-1}) p_k (y_{k-1}|y_1, \ldots, y_{k-2}) \cdots p_{k} (y_1), \\ & = \phi_k p_{\geq k} (y_k | y_1, \ldots, y_{k-1}) p_{\geq k-1} (y_{k-1}|y_1, \ldots, y_{k-2}) \cdots p_{k} (y_1), \nonumber \end{align} \]
| Subject | 6 Months | 18 Months | Age | Race | Baseline |
|---|---|---|---|---|---|
| Subject 1 | \(Y_{11}\) | \(Y_{12}\) | \(x_{11}\) | \(x_{12}\) | \(Y_{10}\) |
| Subject 2 | \(Y_{21}\) | \(Y_{22}\) | \(x_{21}\) | \(x_{22}\) | \(Y_{20}\) |
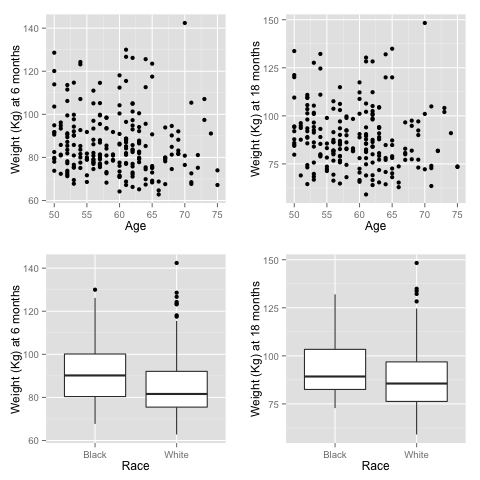
We also did a sensitivity analysis based on an assumption of MNAR.
Specify \(\chi(\mathbf x_{i}, Y_{i1})\) as \[ \chi(\mathbf x_{i}, y_{i1}) = 3.6 + y_{i1}, \]
There are no large differences for estimates for \(Y_2\) under MNAR vs MAR.
This is partly due to the low proportion of missing data in this study.